Bohmian Indeterminism

David Bohm (Photo Credit)
Bohmian mechanics is not just an “interpretation” of quantum mechanics. It is a radical revision. In this note, I’d like to point out one reason that it’s an implausible revision: Bohmian mechanics is rampantly indeterministic in a way that quantum mechanics is not.
Setup: Review of Bohmian mechanics
In Bohmian mechanics, the locations of ![]() particles are described by a point in a real manifold
particles are described by a point in a real manifold ![]() , called the configuration space. The trajectory of a system of particles is a curve
, called the configuration space. The trajectory of a system of particles is a curve ![]() through that manifold. The theory also includes a set of square-integrable functions on this space
through that manifold. The theory also includes a set of square-integrable functions on this space ![]() called wavefunctions.
called wavefunctions.
A physical system in Bohmian mechanics can be characterized by a configuration space ![]() , a wavefunction space
, a wavefunction space ![]() , and also a self-adjoint linear operator
, and also a self-adjoint linear operator ![]() called the Hamiltonian. This Hamiltonian generates a one-parameter group of wavefunctions
called the Hamiltonian. This Hamiltonian generates a one-parameter group of wavefunctions ![]() that solves the Schrödinger equation,
that solves the Schrödinger equation,
![]()
For a given Bohmian system ![]() , an initial condition is a pair
, an initial condition is a pair ![]() , with
, with ![]() and
and ![]() . The fundamental law of Bohmian mechanics then says that, given an initial
. The fundamental law of Bohmian mechanics then says that, given an initial ![]() , the trajectory of the system
, the trajectory of the system ![]() is a solution to the Bohmian Guidance Equation,
is a solution to the Bohmian Guidance Equation,
![]()
where ![]() is the solution to the Schrödinger equation with initial condition
is the solution to the Schrödinger equation with initial condition ![]() .
.
Rampant Bohmian indeterminism
Take as simple a Bohmian system ![]() as you can imagine: a free particle confined to a finite space. It turns out that the Bohmian description is rampantly indeterministic.
as you can imagine: a free particle confined to a finite space. It turns out that the Bohmian description is rampantly indeterministic.
Let the configuration space be ![]() , which describes the possible locations of a particle on a string of finite length. Let
, which describes the possible locations of a particle on a string of finite length. Let ![]() be the set of differentiable square integrable functions
be the set of differentiable square integrable functions ![]() . And let
. And let ![]() , the Hamiltonian for a particle free of any forces or interactions, and where
, the Hamiltonian for a particle free of any forces or interactions, and where ![]() .
.
As a dirt-simple example of indeterminism, choose the initial condition ![]() , and
, and ![]() given by,
given by,
![]()
This wavefunction is square integrable and differentiable. (Square-integrability follows from the fact that ![]() , and differentiability is obvious.) But let’s calculate what the Guidance Equation looks like for this initial wavefunction. Since
, and differentiability is obvious.) But let’s calculate what the Guidance Equation looks like for this initial wavefunction. Since ![]() , the unitary propagator
, the unitary propagator ![]() for our Hamiltonian satisfies
for our Hamiltonian satisfies ![]() . Therefore,
. Therefore,
![]()
The differential equation ![]() is well-known to be indeterministic, following a much-discussed example of John Norton (2008 / animated summary). But let me make it explicit: a Bohmian particle with this initial configuration is compatible with a continuum of future trajectories all satisfying the Guidance Equation. Namely,
is well-known to be indeterministic, following a much-discussed example of John Norton (2008 / animated summary). But let me make it explicit: a Bohmian particle with this initial configuration is compatible with a continuum of future trajectories all satisfying the Guidance Equation. Namely,
![Rendered by QuickLaTeX.com \[ x(t) = \begin{cases} (1/144)(t - T)^4 & \text{for $t\geq T$}\\ 0 & \text{for $t \leq T$.} \end{cases}\]](http://www.soulphysics.org/wp-content/ql-cache/quicklatex.com-a38e0dfb13fd0e0761fd720e175598ae_l3.png)
for any arbitrary time ![]() . (We restrict our attention to times
. (We restrict our attention to times ![]() during which the particle is in the interval
during which the particle is in the interval ![]() , namely
, namely ![]() .) These solutions correspond to a Bohmian particle that sits at
.) These solutions correspond to a Bohmian particle that sits at ![]() up until an arbitrary time
up until an arbitrary time ![]() , when it randomly begins moving.
, when it randomly begins moving.
Not the dome
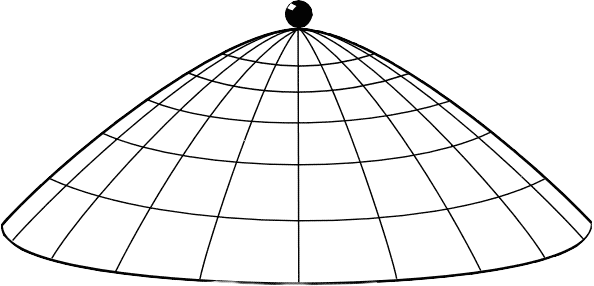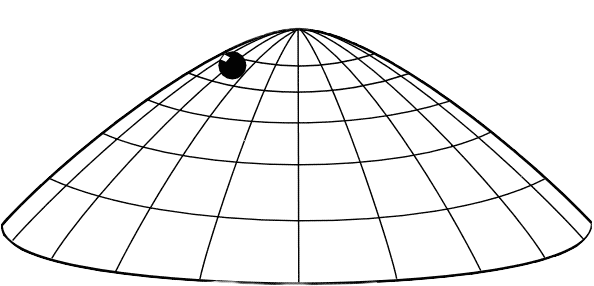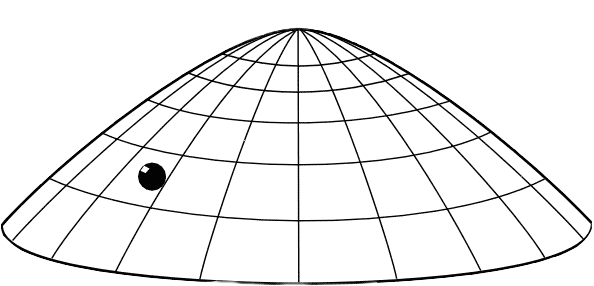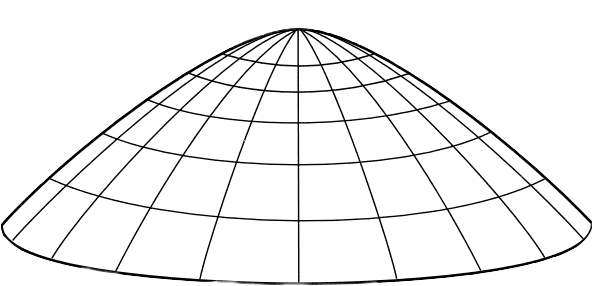
Norton’s Dome (Animation Credit: John Norton)
As a point of comparison, recall that many have complained about the “unphysical” features of the surface of Norton’s dome, such as the infinite Gaussian curvature at the apex (e.g. here and here). No such complaining need be tolerated in the case of Bohmian mechanics. There is no surface to complain about. There is only the wavefunction ![]() , which is a perfectly boring, deterministic wavefunction from the perspective of orthodox quantum mechanics. In particular, it is the initial condition for a unique solution
, which is a perfectly boring, deterministic wavefunction from the perspective of orthodox quantum mechanics. In particular, it is the initial condition for a unique solution ![]() to the Schrödinger equation, which is defined for all times
to the Schrödinger equation, which is defined for all times ![]() . It is only with the addition of the Bohmian Guidance Equation that a pathology occurs.
. It is only with the addition of the Bohmian Guidance Equation that a pathology occurs.
In order to avoid such pathologies, Bohmian mechanics must somehow excise this class of wavefunctions from the theory. But it’s not clear how to motivate this excision in a non-ad hoc way. And it’s even less clear whether it can be done in a way that avoids doing damage to the ordinary quantum dynamics.
This page is full of illogical and erroneous information on Bohm’s incredible interpretation of the Quantum Theory:
1) dx/dt=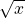 is not “indeterministic” – it’s just a differential equation. Differential equations by themselves say nothing about determinism; they may be chaotic but this one is in fact very simple to solve. You know that x(t) =
is not “indeterministic” – it’s just a differential equation. Differential equations by themselves say nothing about determinism; they may be chaotic but this one is in fact very simple to solve. You know that x(t) =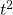 /4 is a solution which is physically real. The particle starts from rest and then accelerates. That random acceleration solution on the dome is unphysical: if the particle is placed at the very top it will never move. Just because a solution is allowed by the differential equation doesn’t mean it’s physically real.
/4 is a solution which is physically real. The particle starts from rest and then accelerates. That random acceleration solution on the dome is unphysical: if the particle is placed at the very top it will never move. Just because a solution is allowed by the differential equation doesn’t mean it’s physically real.
2) Even if what you said about your wave function ψ is correct, does that wave function correspond to a physically real Hamiltonian? What is the potential energy of this hypothetical system? You’ll find that the wave function you have given is impossible because it is not differentiable twice over [-1,1], what you claimed as the domain of integration. The second derivative of ψ is indeterminate at x=0. Every wave function must be differentiable twice in order for it to solve Schödinger’s equation, and the Guidance equation is a consequence of Bohm’s equations being derived from Schödinger’s equation and reproducing Jacobi’s equation, H(S)+dS/dt=0.
In summary: Bohm’s interpretation is in fact deterministic and experimentally equivalent to standard Quantum theory, albeit while painting a radically different and actually sensible picture of the mysterious atomic world.
Hi Jon. On 1): “Indeterminism” is just a synonym to say that the DiffEQ has non-unique solutions for some initial data. I do agree that the dome is pathological, although just calling some solutions “not physical” isn’t quite precise enough for me; some of the precise pathologies are spelled out here.
On 2): The QM Hamiltonian for my system here is just the free-particle Hamiltonian; see the second paragraph. There is no potential energy. My initial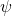 is square-integrable, so it is a perfectly good quantum state in the Hilbert space. It evolves (in ordinary QM) as a simple free wave according to the equation
is square-integrable, so it is a perfectly good quantum state in the Hilbert space. It evolves (in ordinary QM) as a simple free wave according to the equation 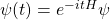 . It is an absolutely trivial and boring quantum system, unless you’re a Bohmian, in which case it is radically pathological.
. It is an absolutely trivial and boring quantum system, unless you’re a Bohmian, in which case it is radically pathological.
This is because wavefunctions don’t need to be twice-differential in QM, and in general they cannot all be when we say that the states form a Hilbert space. Schrödinger’s equation does not require any differentiability conditions when it is cast in its integral form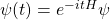 . The unitary operator
. The unitary operator 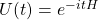 is bounded, and therefore defined on the entire Hilbert space of states, even though the Hamiltonian (and thus the differential form of the equation) is not defined for all states.
is bounded, and therefore defined on the entire Hilbert space of states, even though the Hamiltonian (and thus the differential form of the equation) is not defined for all states.
All of the problems here really do come directly from Bohmian mechanics. In ordinary QM, the system is perfectly non-pathological. I’m afraid I’m not as optimistic as you are about BM!