Philosophy and Physics in the Kadison-Singer Conjecture
A promising proof of the so-called Kadison-Singer conjecture was announced yesterday. Mathematicians are excited, because this conjecture is equivalent to a remarkable number of open problems in other fields. And mathematicians just love to make connections between wildly disparate fields.
Here is another reason to be excited: the Kadison-Singer conjecture has important consequences for the foundations of physics! Settling this conjecture shows an important way in which our experiments are enough to provide a complete description of a quantum system. Here’s why.
Quantum Mechanics: The Simple Picture
The Kadison-Singer question comes out of thinking about how to describe a quantum system. Here is a simplified picture of how that works. When we describe matter in quantum mechanics, there are two main things we are concerned with:
- Observables: Each observable represents a property whose values we can measure, and
- States: Each state is a “probability measure,” which determines the probability of measuring each value of each observable, given our experimental setup.
This is a lot like the situation with a coin: a property that we can measure is the side that is facing up; it can have value “heads” or “tails.” When the coin is in a state of flipping in the air under normal circumstances, the probability of measuring each value is 1/2. So, the state “flipping normally” determines a probability measure. And that measure assigns probability 1/2 to each value that the observable “which side of the coin is facing up” can take.
Quantum mechanics is a lot like that, except we’re measuring the fundamental properties of matter. Our observable might be the spin of an electron, which can take the values “up” or “down.” And our starting state might be an electron flying out of an oven and through a magnetic field. But the principle is the same, and in this case, the state happens to assign probability 1/2 to each value.

Compatible Observables
Now, here is a crucial distinction for understanding the Kadison-Singer conjecture. One thing that is special about quantum observables is that there are some that can be measured simultaneously, and some others that can’t. Two observables that can be simultaneously measured are called “compatible,” and are otherwise called “incompatible.”
For example, you can simultaneously measure position and spin. But you cannot simultaneously measure position and momentum; the latter is known as Heisenberg’s uncertainty principle. Position and spin are compatible observables, but position and momentum are not. This is a simple fact of quantum life. Indeed, according to many, it is the crucial distinction between the quantum and the classical descriptions of the world.
Dirac’s Idea
Dirac suggested a simple formula for taking experiments and using them to describe a quantum system. The following is a slight improvisation on what Dirac actually wrote; the historically-precise may prefer to think of it as a “Dirac-inspired” picture.
We want to know the properties of a quantum system, meaning the probabilities (the states) that get assigned to all the measurable quantities (the observables). How can we use experiments to learn about this? Here is one way.
- Write down what you can measure simultaneously. Collect together a set of compatible observables, and keep adding to it until it is as large as it can be. For example, you could take a finite set of observables (say, position
 and spin
and spin 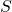 ), and then just add in all the functions of those observables (like
), and then just add in all the functions of those observables (like 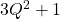 ,
, 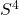 , etc.). The resulting set is called a “maximal abelian algebra.” This set represents the most we can learn from a single experiment.
, etc.). The resulting set is called a “maximal abelian algebra.” This set represents the most we can learn from a single experiment. - Determine the basic probabilities (i.e., pure states). Arrange your lab in some way, and then repeat an experiment that determines the values of those observables. Then do it again. After enough repetitions, you’ll be able to choose a probability distribution for the experiment. A structurally “basic” probability distribution is called a pure state.
- Generalize this information to the entire system. We now want to extend this probability distribution to all the other observables, those that are not compatible with our set. That is, we want to choose a probability distribution that applies to all observables, and which is the same as our probability distribution when restricted to our set of compatible observables. And, if we may ask so much, we’d like this extension to be unique, so that we can be sure we’ve chosen the right one.
The last step is what’s interesting. Dirac’s procedure requires us to extend what we learned about the basic quantum probabilities of compatible observables to all the other observables as well, and to ensure that there is only one way to do so. Is this always possible? That is the Kadison-Singer conjecture.
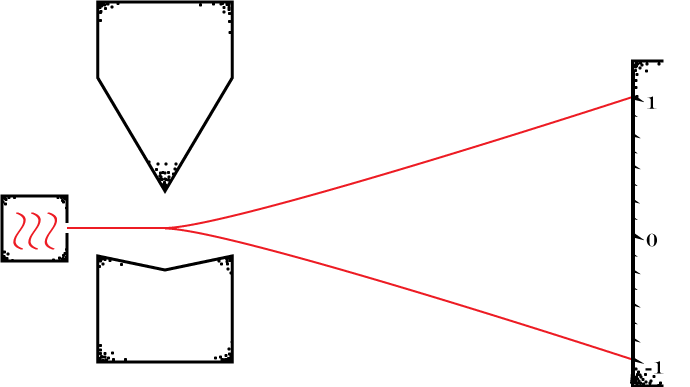
The Kadison-Singer Conjecture
The Kadison-Singer conjecture says we have at least one way to completely characterize a quantum system on the basis of what we can learn from experiments. We can take what we know about the quantum probabilities of simultaneously measurable quantities, and uniquely extend this to all the other measurable quantities as well.
In particular, if we have determined a “basic” probability distribution on a set of compatible observables that is as large as it can be, then this probability distribution extends uniquely to all the other observables.
Here is the precise statement of this claim.
Kadison-Singer Conjecture. Let
be a discrete maximal abelian subalgebra of
, the algebra of bounded linear operators on a separable Hilbert space. Let
be a pure state on that subalgebra. Then there exists a pure extension
of
to all of
, and that extension is unique.
Proof of this statement provides a very nice assurance, that our experiments really are enough to describe quantum systems as we understand them. (Note for those familiar with quantum theory: I have included some notes on the terminology of this statement in the last section of this post.)
Unfortunately, the result is not without caveats, and an important one is the “discreteness” caveat. Although a great many physical descriptions satisfy discreteness, there are also some continuous ones (some of which are relevant to quantum field theory) that are not discrete, and for which the conjecture does not apply. Indeed, Kadison and Singer showed in the second theorem of their original paper that the conjecture fails for such continuous geometries!
History of the conjecture
Kadison and Singer wrote a number of wonderful papers on the mathematical foundations of quantum theory in the 1950’s. The conjecture that is named after them comes from the “Related Questions” section of their 1959 paper on extensions of pure states. On the question of uniqueness, they say that “we incline to the view that such an extension is non-unique.” Kadison and Singer seem to have thought that their conjecture is probably false! You might have expected this too, if you had just proven that uniqueness fails in the continuous case. This makes it all the more surprising that the conjecture turns out to be true.
In settling the Kadison-Singer conjecture, a number of other equivalent propositions are have also been settled. Those familiar with the mathematics of quantum theory may enjoy reading this paper by Casazza and Tremain on some equivalent formulations, which is very accessible from that perspective.
Some mathematical notes
For the statement of the Kadison-Singer conjecture above, here are a few definitions.
We say that an algebra is discrete if it contains “atoms,” i.e. minimal projections ![]() such that
such that ![]() only if
only if ![]() . This is the familiar situation for most. For example, a 1-dimensional projections onto a ray in a Hilbert space is a minimal projection for
. This is the familiar situation for most. For example, a 1-dimensional projections onto a ray in a Hilbert space is a minimal projection for ![]() .
.
A state is a probability distribution that is ![]() -additive on families of mutually orthogonal projections. (Often, one takes a state to be just a positive normalized functional, and defines a state to be normal if it is
-additive on families of mutually orthogonal projections. (Often, one takes a state to be just a positive normalized functional, and defines a state to be normal if it is ![]() -additive.) One of the cornerstones of quantum theory, called Gleason’s Theorem, says that a (normal) state
-additive.) One of the cornerstones of quantum theory, called Gleason’s Theorem, says that a (normal) state ![]() can always be implemented by a density matrix, in that there always exists a density matrix
can always be implemented by a density matrix, in that there always exists a density matrix ![]() such that
such that ![]() for all
for all ![]() .
.
A state is pure if it cannot be expressed as a non-trivial convex combination of other states, i.e., ![]() for
for ![]() only if
only if ![]() . In this sense, pure states are “basic.” The pure states on
. In this sense, pure states are “basic.” The pure states on ![]() can always be implemented by Hilbert space vectors, in that there exists some
can always be implemented by Hilbert space vectors, in that there exists some ![]() such that
such that ![]() for all
for all ![]() .
.
Update
21 June 2013. Orr Shalit at Noncommutative Analysis some very nice comments on the proof of the K-S Conjecture, and Gil Kalai has a nice collection of references.
11 March 2014. Danny points out an interesting example in the comments, which clarifies the importance of requiring that all states be “normal” in the last sentence of this post.
Pingback: The Kadison-Singer Conjecture has beed Proved by Adam Marcus, Dan Spielman, and Nikhil Srivastava | Combinatorics and more
Very interesting post, thanks!
Thanks for writing this! This is the first explanation of the implications of KS in Physics that I’ve understood.
Pingback: What does Kadison-Singer have to do with Quantum Mechanics? | tcs math - some mathematics of theoretical computer science
Pingback: Not mentioned recently on The Aperiodical | The Aperiodical
Pingback: Discrepancy, Graphs, and the Kadison-Singer Problem | Windows On Theory
Pingback: Κβαντομηχανική και εικασία Kadison-Singer | physicsgg
You write: “i.e. minimal projections such that
such that 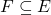 only if
only if 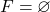 .”
.”
This is simply nonsense.
Nonsense I: What is F here? Ah, seems to be a set. Hence, E must be a set. But first, you say that E is a projection. Set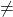 projection.
projection.
Nonsense II: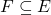 only if
only if 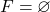 simply implies that
simply implies that 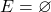 since
since 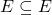 .
.
Also the rest you write is hardly understandable. For example, a functional cannot be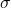 -additive (unless you define this). Only set functions can be
-additive (unless you define this). Only set functions can be 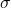 -additive.
-additive.
Hi Fritz. ‘Nonsense’ is a little severe there, isn’t it? In common English, the definition says minimal projections are those that have no non-zero subprojections. Sorry if my notation was confusing. To clarify: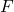 is indeed a projection (not a set).
is indeed a projection (not a set). 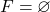 is the zero projection, i.e. the map that sends all vectors in the Hilbert space to the zero vector. The
is the zero projection, i.e. the map that sends all vectors in the Hilbert space to the zero vector. The 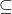 should be interpreted as a proper subprojection here — just substitute
should be interpreted as a proper subprojection here — just substitute 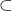 if you prefer.
if you prefer.
The equation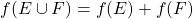 should have the requirement that
should have the requirement that 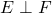 ?
?
Hi Fan, yes. I say that a state is a probability distribution that is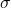 -additive on families of mutually orthogonal projections. That is, a state satisfies
-additive on families of mutually orthogonal projections. That is, a state satisfies 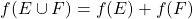 whenever
whenever 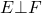 .
.
Pingback: The Kadison-Singer Conjecture explained | The Aperiodical
Bryan,
Unless you have some expanded understanding of what it means to “measure” an observable, I believe that the interpretation of incompatible observables that you present is incorrect.
QM does NOT claim that incompatible observables cannot be simultaneously measured. In fact the incompatible variables of position and momentum of a particle are exactly what is measured in certain EPR-type correlation experiments.
What QM does claim is that one cannot prepare an ensemble of states in which the measurement of the pair of incompatible observables on each member of the ensemble will produce the same results.
This is the content of the uncertainty principle, which is a statement about the joint distribution of repeated results. It is not a statement about any limit on the obtainability of any single result.
Thus, what QM rules out is certain reproducability but does not rule out the ability to obtain a result for any particular case.
The ameliorating note is that precision can only be checked or confirmed though reproducibility.
Thus, one can take the uncertainty principle to be putting a limit on the confirmation of a single measurement.
Furthermore, EPR type experiments show that the problem is not that measurement on a local system “disturbs” that system, since the measurements in EPR are not on localized systems. So the measurement of the momentum of particle A by interacting with particle B does not ‘locally’ disturb some, perhaps simultaneous in some frame, measurement of the position of particle A.
Heisenberg took a few weeks to move from the incorrect to the correct interpretation of his uncertainty principle. It seems that most people still cannot get it straight after 90 years.
This is a great post. One tiny little math error–not every pure state on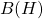 is a vector state coming from some vector
is a vector state coming from some vector 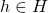 . One way to see this is to take an irreducible representation
. One way to see this is to take an irreducible representation 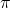 of the Calkin algebra
of the Calkin algebra 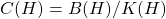 . Composing
. Composing  with
with 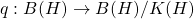 yields an irreducible representation of
yields an irreducible representation of 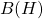 vanishing on compacts, which we also call
vanishing on compacts, which we also call 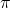 . There is a pure state
. There is a pure state 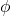 associated to
associated to 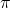 via the GNS construction, by setting
via the GNS construction, by setting 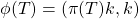 for any unit vector
for any unit vector 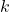 . This state must vanish on compacts, as
. This state must vanish on compacts, as 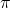 does. But vector states don’t vanish on compacts, e.g.
does. But vector states don’t vanish on compacts, e.g. 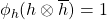 if
if 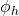 is the vector state associated to the unit vector
is the vector state associated to the unit vector 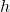 and
and 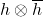 is the projection onto the one-dimensional subspace spanned by
is the projection onto the one-dimensional subspace spanned by 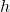 . Thus
. Thus 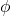 is a pure state which is not a vector state.
is a pure state which is not a vector state.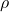 is a pure state on a
is a pure state on a 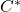 -algebra
-algebra 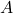 , then there is a representation
, then there is a representation 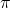 of
of 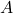 on a Hilbert space
on a Hilbert space 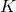 and a unit vector
and a unit vector 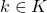 such that
such that 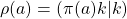 . If the
. If the 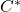 -algebra is “naturally” represented as a collection of operators on some Hilbert space
-algebra is “naturally” represented as a collection of operators on some Hilbert space 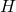 , as
, as 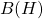 is, you have to be careful to note that this representation might not describe the state as a vector state.
is, you have to be careful to note that this representation might not describe the state as a vector state.
Maybe what you’re looking for is the following statement: if
Hi Danny, thanks for the helpful comment. This is such an interesting example. I think I’ve come across it before, but had certainly forgotten about it. One thing that’s interesting about it is that (unless I’m mistaken) this pure state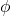 fails to be a “normal” state, i.e., it does not satisfy the condition that
fails to be a “normal” state, i.e., it does not satisfy the condition that 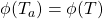 for each monotone increasing set of operators
for each monotone increasing set of operators 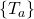 with least upper bound
with least upper bound 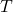 . That condition is equivalent to
. That condition is equivalent to 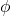 being
being 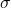 -additive on orthogonal families of projections, which is how I defined normal states in the post above. In fact, I defined states in such a way that they are all normal. This is obviously very limiting mathematically. But I did so because there are some physical reasons to avoid non-normal states in quantum theory. Anyway, that’s a very subtle feature of the argument, which I’m grateful to you for pointing out.
-additive on orthogonal families of projections, which is how I defined normal states in the post above. In fact, I defined states in such a way that they are all normal. This is obviously very limiting mathematically. But I did so because there are some physical reasons to avoid non-normal states in quantum theory. Anyway, that’s a very subtle feature of the argument, which I’m grateful to you for pointing out.
Fantastic layman explanation of the KS Conjecture. Thanks, understood finally. You ought to follow this up with a pop-science book on Quantum Mechanics, in the same style. Congratulations on the receipt of the George Polya Prize.
Opps ! Sorry. Ignore last sentence “Congratulations on the receipt of the George Polya Prize.” – Regards.