Spatial translations in quantum mechanics
I remember that when I first learned the Canonical Commutation Relations in quantum mechanics, they seemed mysterious:
![]()
I knew I was supposed to view this as a law of nature, and that it could be used in some contexts to explain important observations like position-momentum uncertainty. But I remember it being a huge revelation to me when I realized that the canonical commutation relations are just the local expression of spatial translations when space is homogeneous.
This is well-known by experts. But since I couldn’t find an obvious source for it on the interwebs, I thought I’d share the story here for others.
Translations in Space
We want to interpret a self-adjoint operator ![]() as representing position in space. To keep it simple, let’s say it represents position along an infinite length of string, which is easy because it’s 1-dimensional.
as representing position in space. To keep it simple, let’s say it represents position along an infinite length of string, which is easy because it’s 1-dimensional.
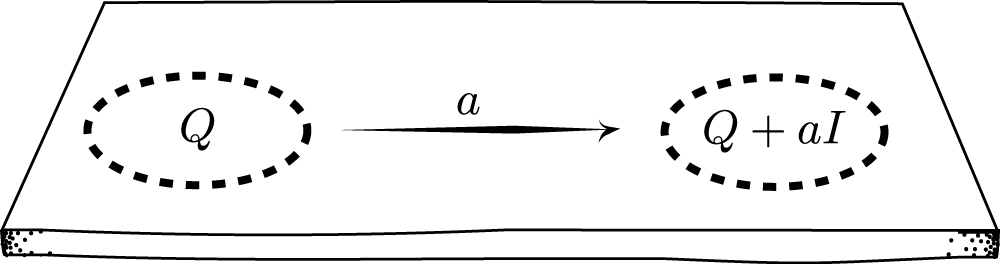
Then we can interpret ![]() as position that has been translated by a distance
as position that has been translated by a distance ![]() in space.
in space.
Now, if space is homogeneous, then no point in space is any different than any other. So, the self-adjoint operators ![]() and
and ![]() are equally good representatives of space. Setting up the same experiment in two laboratories that differ only a distance
are equally good representatives of space. Setting up the same experiment in two laboratories that differ only a distance ![]() will produce the same results.
will produce the same results.
Homogeneity
In quantum mechanics, experimental results are probabilistic, and the transformations that preserve probabilities are the unitary ones. So, we can capture this homogeneity precisely by say that the spatially translated position operators are related by a unitary transformation,
![]()
More can be said about these translation operators ![]() . If we think of the infinite string as continuous, then we’ll want to have a continuous collection of operators
. If we think of the infinite string as continuous, then we’ll want to have a continuous collection of operators ![]() , one for each real number
, one for each real number ![]() . We’ll also want to capture the additive relations between distances on the string,
. We’ll also want to capture the additive relations between distances on the string, ![]() .
.
Whenever this is the case, Stone’s theorem says that there exists a self-adjoint operator ![]() such that
such that ![]() . (Of course we’ve chosen the letter
. (Of course we’ve chosen the letter ![]() suggestively — but wait for it.) So, our statement of homogeneity above can be expressed,
suggestively — but wait for it.) So, our statement of homogeneity above can be expressed,
![]()
The canonical commutation relations
First consequence: this equation implies a special form of the canonical commutation relations known as the Weyl CCRs, ![]() . It only takes one line to check this, so do give it a try. In fact, this equation is equivalent to the Weyl CCRs.
. It only takes one line to check this, so do give it a try. In fact, this equation is equivalent to the Weyl CCRs.
Second consequence: when we take the derivative of both sides with respect to ![]() , we get the normal canonical commutation relations. This is also a nice exercise, which only uses the product rule and the definition of the derivative for exponentials, so I’ll let you give it a go.
, we get the normal canonical commutation relations. This is also a nice exercise, which only uses the product rule and the definition of the derivative for exponentials, so I’ll let you give it a go.
![]()
![]()
Observations
What this means is that the canonical commutation relations in quantum mechanics are the local expression of translations in space — where “local” is in the sense of a derivative, as above. But this should warn you that the derivation needn’t go the other way — in fact, you can’t derive translations in space (or the Weyl CCRs) from the canonical commutation relations.
This is because there is a lot of information in our statement of spatial homogeneity above that is not needed for the CCRs.
For example, we assumed that a dimension of space is described by the entire real line ![]() . But it may be of interest to restrict space to a finite interval of
. But it may be of interest to restrict space to a finite interval of ![]() , or a loop, or even a discrete set of points. As long there space is homogeneous in the sense of there being unitary operators relating the points (and some notion of a derivative can be defined) we can often still construct the commutation relations.
, or a loop, or even a discrete set of points. As long there space is homogeneous in the sense of there being unitary operators relating the points (and some notion of a derivative can be defined) we can often still construct the commutation relations.