Pauli’s Theorem is not a theorem (not as Pauli stated it)

There is a quirk in the literature on time-energy uncertainty. It might have started as a little sloppiness. But it has grown into an error that seems to have spread all over the place.
The incorrect mantra
The problem comes from a footnote in Wolfgang Pauli’s Quantum Mechanics textbook, where he wrote (pg.63, fn.2):
In the older literature on quantum mechanics, we often find the operator equation
… . It is generally not possible, however, to construct a Hermitian operator (e.g. as function of
and
) which satisfies this equation. This is so because, from the C.R. written above, it follows that
possess continuously all eigenvalues fro
to
… whereas on the other hand, discrete eigenvalues of
can be present. We, therefore, conclude that the introduction of an operator
is basically forbidden and the time
must necessarily be considered an ordinary number (“
-number”) in Quantum Mechanics
The conclusion that a time operator ![]() is “basically forbidden” has a strong following. Here’s just a small sampling:
is “basically forbidden” has a strong following. Here’s just a small sampling:
- “In quantum mechanics there is in fact no self-adjoint time observable of any suitable sort” (Dürr, Goldstein and Zanghi, pg. 12)
- “In
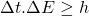 , only the energy is a physical quantity like
, only the energy is a physical quantity like  and
and 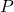 ;
;  , on the other hand, is a parameter, with which no quantum mechanical operator is associated” (Cohen-Tannoudji, Diu and Laloë, vol.1 pg. 251)
, on the other hand, is a parameter, with which no quantum mechanical operator is associated” (Cohen-Tannoudji, Diu and Laloë, vol.1 pg. 251) - “time enters into Schrödinger’s equation, not as an operator (i.e., and “observable”) but rather, as a parameter” (Aharanov and Bohm).
These statements are strictly false. Although people often repeat Pauli’s conclusion that there can be no time operator ![]() in quantum mechanics, they are not stating a theorem.
in quantum mechanics, they are not stating a theorem.
A counterexample
Here is a simple counterexample, which was pointed out by Busch, Grabaowski and Lahti (1994), but which apparently had little impact on the broader physics community.
Let ![]() , and consider the Hamiltonian
, and consider the Hamiltonian ![]() . Define
. Define ![]() . Then by a trivial calculation,
. Then by a trivial calculation,
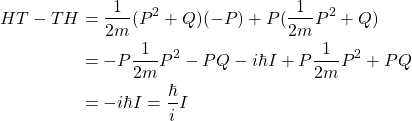
This ![]() is a time observable by Pauli’s own definition. It is not “forbidden.” It would be best if everyone stops saying that it is.
is a time observable by Pauli’s own definition. It is not “forbidden.” It would be best if everyone stops saying that it is.
What to say instead
Before the erroneous conclusion, Pauli’s original passage says something like, “systems with discrete energy do not admit a time observable.” This isn’t a very powerful thing to say, since many interesting physical systems (like the free particle) have a continuous energy spectrum. But more importantly, this statement is also incorrect. Garrison and Wong proved back in 1970 that the harmonic oscillator (which has a discrete energy spectrum) does allow for a self-adjoint operator ![]() satisfying the commutation relation above.
satisfying the commutation relation above.
A more interesting (and correct) thing to say is that if ![]() is bounded from below, then there can be no self-adjoint operator
is bounded from below, then there can be no self-adjoint operator ![]() that satisfies the relation,
that satisfies the relation,
![]()
This was proved rigorously by Srinivas and Vijayalakshmi (1981). Equivalently, it says that there is no self-adjoint operator conjugate to ![]() in the sense of the Weyl commutation relations.
in the sense of the Weyl commutation relations.
But perhaps most intuitively, the result says that if energy is bounded from below, then there can be no self-adjoint operator that continuously tracks the value of the time parameter ![]() describing the system’s unitary evolution.
describing the system’s unitary evolution.
All known physical systems have energy that is bounded from below. In fact, most of them have energy that is always positive! So, a more correct slogan for the community to adopt would be this:
In all physical systems in which energy is bounded below, there is no self-adjoint observable that tracks the time parameter
.
This slogan excludes the counter-example above, because that Hamiltonian does not describe any known physical system, as its energy is unbounded above and below.
I first learned about many of these results from my friend Tom Pashby, who has written a very interesting dissertation on this topic. Some of his work has been summarized here.
I didn’t know this was called Pauli’s Theorem! Pauli should have read my webpage on this subject.
@John — Thanks for the link, it’s incredibly clear as usual! Just a small quibble: the uniqueness theorem you refer to holds only of the Weyl form of the commutation relations. A representation satisfying![Rendered by QuickLaTeX.com [A,B]=i\hbar](http://www.soulphysics.org/wp-content/ql-cache/quicklatex.com-a3038f141b7a9f2d199f45e39cd459a1_l3.png) need not be unitarily equivalent to the Schrödinger representation if
need not be unitarily equivalent to the Schrödinger representation if 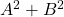 is not densely defined. (There’s a nice discussion of this in Blank, Exner and Havlicek’s textbook.) But this doesn’t really effect your main argument for about the meaning of
is not densely defined. (There’s a nice discussion of this in Blank, Exner and Havlicek’s textbook.) But this doesn’t really effect your main argument for about the meaning of 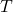 , since the Weyl form of the CCR’s for
, since the Weyl form of the CCR’s for 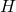 and
and 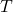 also implies that
also implies that 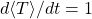 .
.
>> All known physical systems have energy that is bounded from below.
Well, Dirac invented the “sea of electrons” to fill all states with negative energy in his model. So there is one way around this loophole (mixed metaphor alert!) …
Ha. A loophole indeed. That’s a good point. On the other hand, since the Dirac sea requires unbounded energy in the vacuum, I suppose it’s not very realistic from a gravitational perspective. But I defer to the experts in the comments on such matters.
Hi Bryan,
It’s a nice post with many good references. However, I don’t quite see why Pauli’s main point is an error, eve if you could argue that his statement was not in a rigorously mathematical manner. Regarding of this, l would like to mention one point: the CCR equation
is the sufficient condition to the “translation” relation
Therefore, the non-existence of the “translation” relation must indicate the non-existence of the CCR. This is what essentially Pauli’s theorem says about.
Hi Xu,
The implication you suggest does not generally hold: the ordinary Heisenberg CCR does not imply the Weyl/translation form of the CCR.
This is essentially due to domain subtleties with these unbounded operators. You can find a discussion e.g. in Garrison and Wong (1970). One can however introduce further conditions under which these two commutation relations are equivalent; this was worked out by Nelson (1959). You can find a discussion of how to interpret those extra conditions in Thomas Pashby’s recent dissertation, page 93.
But this is all apart from the main reason I think Pauli’s statement is incorrect, which is because he doesn’t recognize the need to assume a positive-energy condition.