What is a superselection rule?
A superselection rule is a special limitation on what is observable in the quantum world. For example, we can never seem to observe interference from the relative phases between a boson and a fermion. This can be seen as a consequence of a superselection rule.
However, there are lots of ways to make the limitation of a superselection rule precise, and the literature is sometimes confusing as a result. To help keep things straight, John Earman (2008) started off a very rich article with five ways to express the presence of a superselection rule. I find John’s classification helpful, and so I thought I’d share a little summary. I’ll then briefly mention the fermion-boson superselection rule as an example, and end with some warnings about common mistakes.
Superselection rules: 5 expressions
John describes five basic characterizations of a superselection rule that are all mathematically equivalent. They’re expressed in the language of operator algebras, the rigorous mathematical language of modern quantum theory.
Let ![]() be an algebra of bounded linear operators acting on a Hilbert space
be an algebra of bounded linear operators acting on a Hilbert space ![]() . Note that it may in general be a proper subalgebra of the set of all bounded operators
. Note that it may in general be a proper subalgebra of the set of all bounded operators ![]() . The pair
. The pair ![]() is said to have a superselection rule if any of the following are true.
is said to have a superselection rule if any of the following are true.
- SSRI.
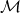 acts reducibly on
acts reducibly on 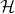 , meaning that its action leaves a non-null proper subspace of
, meaning that its action leaves a non-null proper subspace of 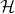 invariant.
invariant. - SSRII. The commutant
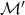 , which is the set of all bounded linear operators that commute with everything in
, which is the set of all bounded linear operators that commute with everything in 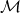 , contains operators besides the constant multiples of the identity.
, contains operators besides the constant multiples of the identity. - SSRIII. For any normalized vector states
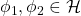 and any unitary operator
and any unitary operator 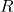 such that
such that 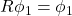 and
and 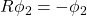 , the superposition
, the superposition 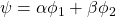 (with
(with 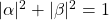 ) is a mixed state.
) is a mixed state. - SSRIV. The Hilbert space
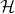 has subspaces
has subspaces 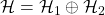 such that no observable
such that no observable 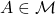 has non-zero matrix elements in both subspaces; i.e., for all
has non-zero matrix elements in both subspaces; i.e., for all 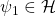 and
and 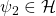 ,
, 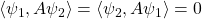 .
. - SSRV. The Hilbert space
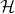 has subspaces
has subspaces 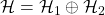 such that the relative phases between the two subspaces are unobservable; i.e., if
such that the relative phases between the two subspaces are unobservable; i.e., if 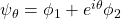 and
and 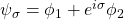 , then
, then 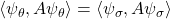 for all observables
for all observables 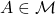 .
.
The boson-fermion superselection rule
An example of a superselection rule, mentioned above, is the so-called Boson-Fermion Superselection Rule. This was the first known superselection rule, discovered in a famous (1952) paper by Wick, Wightman and Wigner.
If you have a single boson and a single fermion, these particles occupy a Hilbert space of the form ![]() . Let
. Let ![]() be a vector state of the boson, and let
be a vector state of the boson, and let ![]() be a vector state of the fermion.
be a vector state of the fermion.
As you may know, if you time reverse a boson twice, it goes back to where it started. But if you time reverse a fermion twice, it picks up a negative sign. That is,
![]()
That’s an inevitable fact of quantum life. But it still seems to be the case that no measurable quantities are changed under the transformation ![]() , and so we seem to have physical grounds to believe that
, and so we seem to have physical grounds to believe that ![]() for all observables
for all observables ![]() . This gives rise to a superselection rule, in all of the senses above.
. This gives rise to a superselection rule, in all of the senses above. ![]() is the relevant non-constant operator for SSRII and SSRIII, and
is the relevant non-constant operator for SSRII and SSRIII, and ![]() are the relevant subspaces for SSRIV and SSRV. It is a good exercise to check that all these superselection rules follow. But if you get stuck, many of the calculations can be found in textbooks like Ballentine (1998).
are the relevant subspaces for SSRIV and SSRV. It is a good exercise to check that all these superselection rules follow. But if you get stuck, many of the calculations can be found in textbooks like Ballentine (1998).
Words of warning
It’s easy to slip up with superselection rules, especially when time reversal is involved. Here are two words of warning to keep an eye out for.
1. There’s sloppy language out there. Notice that none of the expressions of a superselection rule above imply that a superposition of a boson and a fermion is “impossible” or “not realizable.” Experts often say this when they’re being sloppy, but it has a tendency to confuse students. The best thing to say is that we are limited in what we can observe about the superposition of a boson and a fermion, in the sense of SSRI-V above. Nothing more.
2. Time reversal invariance has nothing to do with it. Following Wick, Wightman and Wigner, I said above that the boson-fermion superselection rule follows from the way that two successive applications of the time reversal operator transform fermions and bosons, and the fact that ![]() for all observables
for all observables ![]() . I did not assume time reversal invariance, which says that
. I did not assume time reversal invariance, which says that ![]() where
where ![]() is the Hamiltonian, and this assumption is not needed. That’s good, because time reversal invariance has been known to fail since the 1964 discovery of T-violation by James Cronin and Val Fitch.
is the Hamiltonian, and this assumption is not needed. That’s good, because time reversal invariance has been known to fail since the 1964 discovery of T-violation by James Cronin and Val Fitch.
And yet, in a very strange historical episode, Hegerfeldt, Kraus and Wigner (1968) declared that the Wick-Wightman-Wigner argument is invalid because it relies on time reversal invariance. Earman follows them in this mistake (pg.379), as do many others.
But this declaration is simply wrong. Time reversal invariance has nothing to do with it. Just do the derivation to see what I mean, or look at the original Wick, Wightman and Wigner. Or, more intuitively, notice that superselection rules are properties of the “kinematics” or observable structure of a quantum system. Invariance under time reversal is a property of the “dynamics” or time evolution of that system. The observation that ![]() can be a perfectly good constraint on the kinematics, whether or not
can be a perfectly good constraint on the kinematics, whether or not ![]() is a property of the dynamics.
is a property of the dynamics.
- Philosophy and Physics in the Kadison-Singer Conjecture
- Pauli’s Theorem is not a theorem (not as Pauli stated it)
