Solving the Black Hole Information "Paradox"
 In January, Abhay Ashtekar posted a short preprint in which he (along with two collaborators) proposed a new solution to the so-called black hole information paradox in 1+1 dimensions. Their essential trick is to propose a quantum-gravity inspired framework in which there is no black hole singularity, which leads to no loss in quantum information. This paper received a lot of superficial attention in the media last week; here’s a little background on what’s going on.
In January, Abhay Ashtekar posted a short preprint in which he (along with two collaborators) proposed a new solution to the so-called black hole information paradox in 1+1 dimensions. Their essential trick is to propose a quantum-gravity inspired framework in which there is no black hole singularity, which leads to no loss in quantum information. This paper received a lot of superficial attention in the media last week; here’s a little background on what’s going on.
Background: Black Hole Entropy.The theory of black hole entropy is a well accepted combination of general relativity and quantum theory, which exploits the following close analogy between black hole physics and thermodynamics:
- black hole mass :: energy of a thermodynamic system;
- surface area of the event horizon :: entropy;
- surface gravity k :: temperature.
The last analogy is more than that: a black hole’s surface gravity is literally its temperature. A black hole radiates energy exactly like a black body, with temperature k/2π, where k is the surface gravity of the black hole. This effect, called Hawking radiation (which I have discussed before), entails that eventually, all black holes will radiate away their mass, until they become boring everyday objects.
The Problem. The problem that many have with this process is that, according to a semi-classical analysis first argued by Stephen Hawking, it entails an unusual loss of quantum coherence. Here’s a very informal sketch of how it happens.
Consider two particles that are initially correlated. One particle enters the event horizon of the black hole, while the other remains outside. Informally, it appears that half of the initially correlated state will disappear into the black hole singularity. So after the black hole has completely evaporated, we will have “lost” all information about the correlation. The result: the correlation is broken, and we are left with a mixed state.
In ordinary quantum mechanics, there is no mechanism for a state to evolve from pure to mixed in this way. As a result, many take the appearance of this phenomenon in black hole physics to be a fundamental problem for quantum gravity. The phenomenon is even sometimes referred to as a “paradox,” although this is pretty inappropriate, since it doesn’t seem to give rise to any contradiction. After all, the analysis doesn’t actually use ordinary quantum mechanics, but rather quantum field theory.
In quantum field theory, the evolution of a state from pure to mixed is a pretty ordinary phenomenon. It certainly isn’t unique to the highly curved spacetimes around black holes; in fact, curved spacetimes aren’t even required to produce the effect! For example, Wald (1994, chapter 7.3) shows how this phenomenon can occur in (flat) Minkowski spacetime. Here’s the trick.
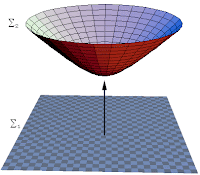
Consider a massless scalar field that is spread out across all of space (i.e., on a Cauchy spacelike hypersurface); call this the initial (pure) state. Suppose this field evolves into a hyperboloid, or any other non-Cauchy hypersurface; call this the final state (see figure below). Then instead of radiation falling into a black hole, there is radiation propagating out to infinity. As a result, the correlation of the field on the interior domain of dependence of the hyperboloid is only “correlated” with radiation at infinity, and so is really in a mixed state.
This is the same “paradox” of quantum information, but in flat spacetime: a pure quantum state evolves into a mixed state. It’s not a paradox that is somehow unique to strong gravitational systems. It is a very general feature of quantum field theory.
If one simply accepts this fact, then it is far from clear that the Black Hole Information “Paradox” is much of a problem at all.
Solving the Problem Anyway. If it’s not clear that there’s a problem, then why are people proposing so many solutions? Well, perhaps the rhetoric of solving a problem is misplaced here. Perhaps a better characterization would be that most physicists are trying to extend a theory. In both black hole evaporation and in the hyperboloid field evolution described above, the essence of the phenomenon is this:
the final state of some quantum field provides an “incomplete” description of the original field.
So any effort to solve the problem is really an effort to give a more complete description of the field. And much of the physics community now agrees that such a description should be available.
Now that we’ve got a better grip on what we’re actually “solving” here, we can ask: what have Ashtekar and his collaborators brought to this discussion? The solution of Ashtekar et al. draws on ideas from Loop Quantum Gravity (LQG), one of the major competitors of string theory. LCG has recently received attention for its apparent ability to resolve certain kinds of singularities (for example, LCG can resolve the big bang singularity).
What Ashtekar et al. have shown is that, given a suitable quantization of spacetime, black hole singularities can also be resolved. In this framework, no part of the original field “disappears” into a singularity because there is no singularity. Therefore, no information is lost, and a pure state remains a pure state.
As discussed above, this doesn’t mean that quantum information loss can’t happen; it only suggests a framework in which it doesn’t happen as a result of black hole evaporation. Whether or not any such framework can prevent quantum information loss altogether remains to be seen.
Soul Physics is authored by Bryan W. Roberts. Thanks for subscribing.
Want more Soul Physics? Try the Soul Physics Tweet.
Here’s a nice (1995) survey of the “black hole information paradox.” It’s a bit outdated, but still very informative.