Special Relativity and the Bell Theorems
The Bell Theorems, together with a collection of experimental results (such as those of Aspect et al.), provide good statistical evidence that quantum theory is “non-local.” Roughly, this means that the interaction between two bodies in quantum theory doesn’t necessarily get weaker as those bodies become spatially separated.
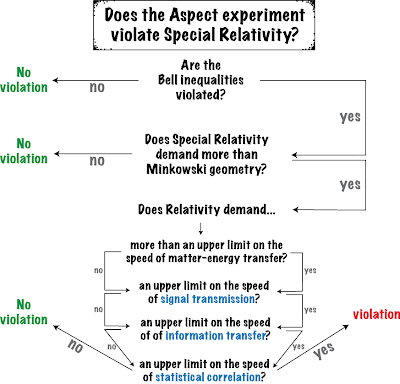
Is this a problem for Special Relativity? That depends on what you think Special Relativity means. Here’s a simple flow-chart illustrating some of what’s at stake.
For a very accessible view on how we should navigate many of these options, I highly recommend Tim Maudlin’s excellent book on the subject. But here are a few thoughts on each of the steps.
-
Bell-inequality violation. There is a sect of conspiracy theorists who aren’t convinced that the Bell-inequalities are violated by experiment. If that’s you, then there’s no reason to worry about Special Relativity.
- Minkowski Geometry. If Special Relativity requires only that the background spacetime be Minkowski spacetime, then there is no problem for non-local quantum effects. After all, we have plenty of matter theories (quantum field theories) that take place on such a background, and even respect its symmetries to a certain extent. Non-locality is not a problem here.
- Upper limit on the speed of mass-energy transfer. We would normally like to add that matter-energy cannot be transferred faster than the speed of light. But this is not a problem for quantum non-locality, either — unless you adopt a pretty unusual view of matter-energy transfer. Then what matters is statistical correlation — see below.
- Signal/Information Transfer. These terms are a bit vague, and people disagree about how to explicate them. However, as the chart suggests, I think that what’s really important is whether or not you think there are consequences for the statistical behavior of distant regions.
- Statistical Correlation. This seems to be the heart of the problem. If you think that Special Relativity implies an upper limit on the “speed” at which statistical correlation can occur, then you’ll think the Bell-type results violate this. What I mean by that is: interactions in one region can have near-immediate consequences for the statistical behavior of another region, no matter how far apart the two regions are.
But why would someone answer “yes” to the last choice in the chart? Why should we think that Special Relativity implies anything at all about the statistical behavior of matter?
There is no probability measure in SR. Of course, matter satisfying the assumption of local realism appears consistent with Special Relativity, and the Bell inequalities hold for such matter. But I see no reason to think that such matter is required by Special Relativity. If it isn’t, then Special Relativity isn’t enough to derive the Bell inequalities, and doesn’t contradict non-locality.
And that’s exactly how we all like it. Right?
Soul Physics is authored by Bryan W. Roberts. Thanks for subscribing.
Want more Soul Physics? Try the Soul Physics Tweet.
I’m not sure how the last condition is relevant at all. Maybe I’m misunderstanding things, though. Here’s what I’m thinking.
Suppose you and I decide to do an experiment. We get outside each others’ light cones, and each flip a coin 100 times, recording the way each flip happened to come out. We come back together and compare our results, and find that our flips were PERFECTLY anti-correlated: every time your coin came up heads, mine came up tails (and vice-versa).
That’s a very interesting outcome, and it’s one that’s statistically quite unlikely. Still, there doesn’t seem to be any reason to think that relativity has been violated, or that there’s been some kind of superluminal information exchange between the coins: it’s just a coincidence about how two events that were space-like separated happened to come out when compared against one another. If the two events were genuinely stochastic, then there doesn’t seem to be any reason at all to suppose that the flip of one coin affected the flip of the other–an intuition we’d expect to be born out if we repeated the experiment a few times.
There are, as far as I can see, two possible ways to read the “limitation on superluminal correlation” condition. The first one is just as above: correlation between distant stochastic events. I don’t see how that could possibly be taken to have anything to do with relativity, and I’m not even sure how to make sense of a locution like “the speed of statistical correlation.” Either the two outcomes are correlated or they aren’t: correlation is a purely local (it seems to me) phenomenon, at least in that it doesn’t depend (in any non-trivial way) on distant events. Identifying two events as correlated, that is, is just to list a set of facts about one event and a set of facts about each event, and then to note that there’s a particular statistical relationship between those two outcomes: a statistical relationship, though, doesn’t need to “travel” anywhere.
The other way that the last condition might be read is as a correlation between hidden (and perhaps non-stochastic) variables–the EPR way of looking at it. That, though, seems to be precisely what Bell showed can’t possibly be at work here.
I’m sure I’m missing something here, but I can’t figure out what it is. I just don’t know how to think about that last condition in a way that fits it in with the rest of this flowchart (which is quite nice, by the way!). Help is always appreciated :)
Yeah, I wasn’t sure how to appropriately word that last condition, so I just tried to clarify it in the commentary below the chart. I guess I should emphasize, what I meant by that last condition is that:
“interactions in one region can have near-immediate consequences for the statistical behavior of another region, no matter how far apart the two regions are.”
That *is* the kind of correlation pointed out by EPR, but it’s *neither* of the two options you suggest. I hope that helps.
Good, that’s helpful! That seems right, but it seems strange to call that mere ‘correlation.’ If interactions in one region have CONSEQUENCES for what’s going on in another region, that’s far more than mere correlation (that’s the sort of case, it seems to me, that I outlined with the coin-flip example). Just calling it “causation,” though, seems almost to beg the question at hand. Maybe “superluminal counterfactual dependence?” Again, though, it seems odd to think about things that way: counterfactual dependence doesn’t (on the face of it) look like the sort of thing that could have a velocity, superluminal or otherwise.
Thanks!
I don’t appreciate being called a conspiracy theorist, Bryan…
It’s nothing personal Noah. ;)
Bryan talked about “the speed at which statistical correlation can occur”. Would please let me know how experimentally can we measure the “speed” of occurrence of statistical correlations? And in which experimental investigations of Bell theorem such speed has been measured?
And also what does it mean when we said “a theory is non-local”?
There are many precise ways to interpret non-locality. For now, I’ll stick with the rough terminology that I wrote above:
“Roughly, this means that the interaction between two bodies in quantum theory doesn’t necessarily get weaker as those bodies become spatially separated.”
The speed of “statistical correlation” can be measured by calculating the speed at which statistical behavior can be changed by an interaction — in particular, by measuring the distance between some system exhibiting statistical behavior (such as a beam of photons) and an interaction (such as the measurement of another beam), and dividing that by the time required for the change to occur. Notably, if the time required can be shown to be arbitrarily small, then the “speed of correlation” can be seen to be arbitrarily large.
The interaction between two bodies in quantum theory (QM) does get weaker as two bodies become spatially separated. However, the correlations between the statistics of the corresponding measurements on them do not! You should carefully distinguish two conceptions: the correlation and the interaction. For a two-body system, the interaction is described by a unitary operator which is not a tensor product of two other unitary operators, and the correlation function is usually described by joint probabilities. For entangled systems, the results of measurements on a system together with the results of measurement on other spatially-separated systems (i.e., the coincidence rates described by joint probabilities) show the spooky dependency on the parameters of both systems. However, when the outcome of the measurements on a single system are taken into the account (i.e., the individual rates described by marginal probabilities), no dependency upon the measurements of the other spatially-separated system appears. In other word, no change in the quantum mechanical statistics of a system take place as a consequence of the interactions (e.g., measurement) with the other remote systems.
In my idea, the way you rephrase Bell theorem and its consequences misses some subtle and delicate issues. I would try to explicitly explain what I mean in the following paragraph, however in accord with non-relativistic QM:
It is usually believed that if two events A and B are correlated, then the correlation between A and B is either due to a direct causal influence connecting A and B, or there is a third event C which is a common cause of the correlation. However, it seems that both of these scenarios are problematic in Quantum domain. In some occasions, QM predicts the correlation between measurements statistics of two systems which are spatially separated. The celebrated Bell theorem together with the experimental investigations led to the customary conclusion that these spooky quantum correlations cannot be explained based on the combined assumptions of separability and locality. What does it mean? Does this means that there an apparent contradiction at the deepest level between two pillars of physics, QM and relativity? Now, here your flowchart could be useful.
However, QM seems to contain some implicit principles that constrain quantum non-locality in ways that finally make the peaceful co-existence between quantum and relativity. The quantum mechanical arguments against superluminal signaling, usually referred as quantum no-signaling theorems, suppose that quantum nonlocality can be demonstrated in a direct way only if the local operations have observable effects (i.e., changing the probability distribution) in a causally disjoint (i.e., space-like) regions. In other word, quantum non-locality can be experimentally manifested if “interactions in one region can have … consequences for the statistical behavior of another [spatially-separated] region”. Hence, these theorems show that for these schemes to work, they must involve processes incompatible with the principles of QM (e.g., the cloning of quantum state or a non-unitary evolution). Consequently, the signaling is refuted according to the mathematical foundations of non-relativistic quantum theory.
Hi MB,
You’re right that it’s important not to confuse unitary interaction with correlation — perhaps the chart could be clearer on this point. I of course meant “interaction” in a more general sense, something like “to have observable effects.”
I think we agree that the main difficulty lies in the meaning of “locality.” The different options on my chart can be seen to correspond to different meanings for this word. But, as you point out, there are further precise characterizations (and even some guarantees) of locality provided by the no-signaling theorems in QFT — even before we turn to the interpretation of relativity. Thanks!
I´m ignorant about physics so just delete this comment if it´s stupid; but if
“interactions in one region can have near-immediate consequences for the statistical behavior of another region, no matter how far apart the two regions are”,
don´t people find that somewhat strange, and isn´t such correlation bound to be taken as due to a causal connection? And wouldn´t we then have the problem of explaining a connection that is “faster” than SR allows?
All comments are welcome Ape. (1) People do find that strange; (2) it’s not really clear if the correlation stems from a causal connection, because there’s no consensus on the precise meaning of “causal” in science; (3) SR might technically allow for travel faster than the speed of light — what it does forbid is *acceleration* from a speed slower than light to a speed faster than light. Some people like to add further restrictions to SR, as indicated on the chart above — but there’s no clear agreement on what should be added, if anything.
Thanks for the clarifications. My hunch is that these correlations will be taken by physicists as causal, or as something more or less causal, whether mediated by tachyons or by immediate affinity of some funky sort. For even though there is no consensus on what “causal” means, scientist won´t accept massive statistical correlation without underlying rationale. Well, perhaps they do accept that for technical reasons, but in their hearts they think there is a cause behind the correlation. Or am I just projecting on them my own primitive gut-feeling?
Step back and try to understand Einstein’s notion of “practical geometry” as an expression of constructivism. It’s obvious you don’t understand current ideas regarding constructivist math and how Einstein used it in formulating the relativity of simultaneity. Good place to start is A. Garciadiego, BERTRAND RUSSELL AND THE ORIGINS OF THE SET-THEORETIC ‘PARADOXES.’
But remember, humble yourself: you are VERY ignorant of recent work in the history of mathematics and its implications for the mathematical approach of the relativity of simultaneity.
So take a deep breath, put your ego to one side, READ and THINK, then try to come up with some reply.
Ryskamp, John Henry, Paradox, Natural Mathematics, Relativity and Twentieth-Century Ideas (June 17, 2008). Available at SSRN: http://ssrn.com/abstract=897085
Locality is a tricky subject. I define it by using clocks, relative my observations. Einstein used a definition in where he sent a light beam to a mirror, that then reflected it back to the Source&receiver, which then by splitting this two way ‘communication’ gave him a ‘local’ speed of light, relative his own clock.
That one should hold in all situations, accelerating or not, as long as you measure it the exact same way, ‘locally’ as I assume.
We also have NIST experiments in where they proved time dilations, due to the gravity on Earth, existing at such distances as half a meter. Assuming ideally sensitive clocks and also assuming that the shortest measure of a light ‘distance’ making physical sense is one Planck length in one Plank time we can get a definition of a ‘frame of reference’, related to ‘clocks’ observed relative your ‘local’ clock that in this case best is describe conceptually.
That also should give us a possibility to define a ‘time dilation’, and so discount it, to describe a ‘one way speed’ of radiation relative you observing, which then should be ‘c’ in a vacuum. Well, as I think of it :)
But as the ‘frame of reference’ for your ‘local clock’ then is one Plank length ‘big’ a frame of reference relative any ‘clock’, yours or some others, becomes a tricky definition, except in the case with the two way definition Einstein used, in where we can assume the detector to also be the ‘local clock’, as I think of it.
And that’s sort of sad. I would have preferred a simpler way of defining ‘locality’, because even if using my definition you to define a ‘one way’ definition you then have to accept that what ever ‘clock’ you use locally also will be influenced by its location relative you observing it ‘tick’.
All as I think of it.
Yoron.