How to time-reverse a quantum system
Time-reversing a classical Newtonian trajectory is simple. If q(t) and p(t) are the positions and momenta of a particle on the trajectory, then time reversal flips that trajectory as follows:
- q(t) → q(-t) = q(t)
- p(t) → p(-t) = -p(t)
For example, a particle traveling along some path with velocity to the left becomes a particle traveling along that path with velocity to the right — just like when we play a movie in reverse. Very simple.
In quantum mechanics, time-reversal looks comparatively strange, because it involves complex conjugation. (More precisely, it is implemented by an antiunitary Hilbert space operator.) Why? Here’s my answer today (more answers later):
One reason that time reversal in quantum mechanics requires complex conjugation is that time-reversing a wave function requires time-reversing its phase.
I recently pointed out an oversimplified way to visualize certain wave functions. Here’s a better way to put the idea: The phase of a simple plane wave can be visualized as the assignment of a “dial value” to little regions in spacetime.
In particular, if the plane wave (in the position representation) has the form:
then exp(-it) — the phase — is just a point on a circle, lying on the complex plane. So, we can think of ψ(x, t) as assigning dial-values to points — each corresponding to a different location on the circle. Moving smoothly forward through time gives rise to a changing dial value. This just represents the changing phase as the plane wave propagates through space:
Now, how should we time-reverse such a system? Well, minimally, it seems we’d want our dial to run in reverse. That’s exactly what conjugation does. Notice that by sending ψ to its conjugate ψ*, we flip the arrow about the real axis of the dial:
The result is an arrow moving in the opposite direction. Moreover, the arrow cannot be reversed by any symmetry operator that does not conjugate (i.e., a unitary operator). That’s because the wavefunction ψ(x, t) is given by an inner product, and unitary operators preserve inner products.
So there you have it: one way to see why quantum time-reversal requires conjugation.
As a final note: a wave’s phase really just describes its relationship to the origin of a coordinate system. So, one might complain that phase isn’t a physical feature of a wave, any more than a coordinate system is. However, differences in phase, and in particular changes in phase, are physical features of a wave. So, our account of time reversal must be sure to reverse these quantities as well.
Soul Physics is authored by Bryan W. Roberts. Thanks for subscribing.
Want more Soul Physics? Try the Soul Physics Tweet.


Nice article, but I want to ask what happens if a system is dissipating? Will complex conjugation suffice as
Time reversal operation ?
Yes it will. Although a dissipating system fails to be time reversal invariant, the meaning of time reversal remains the same: fix position, and reverse momentum, reverse phase.
The only time when complex conjugation does not suffice is when one introduces degrees of freedom into the system that are not functions of position or momentum. Like spin. To get an intuition as to why complex conjugation is not enough to time reverse a fermion, just think about what happens to the Pauli matrices when you conjugate them:
Only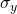 changes sign. But really all the Pauli matrices should change sign under time reversal, since they all represent a kind of angular momentum. So, conjugation is not enough. The standard time reversal operator for a fermion turns out to be not only conjugation, but also multiplication by
changes sign. But really all the Pauli matrices should change sign under time reversal, since they all represent a kind of angular momentum. So, conjugation is not enough. The standard time reversal operator for a fermion turns out to be not only conjugation, but also multiplication by 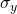 . That is, if we write
. That is, if we write 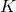 to represent conjugation for position wavefunctions, then time reversal has the form
to represent conjugation for position wavefunctions, then time reversal has the form 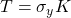 . One can check that this operator does reversal all the Pauli matrices,
. One can check that this operator does reversal all the Pauli matrices,