Map of the Cosmic Acceleration Literature
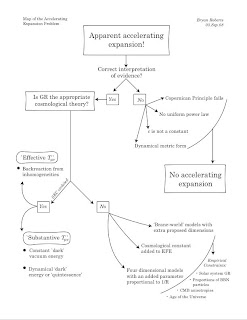 Ten years ago, the physics community came to agree that the expansion of the Universe is experiencing a positive acceleration. The experts still disagree on why. Everything but the kitchen sink has been proposed (I’ve mentioned this twice before), but there is a paucity of experimental evidence to favor one proposal over another.
Ten years ago, the physics community came to agree that the expansion of the Universe is experiencing a positive acceleration. The experts still disagree on why. Everything but the kitchen sink has been proposed (I’ve mentioned this twice before), but there is a paucity of experimental evidence to favor one proposal over another.
This situation strikes me as a gold-mine for philosophers physics. In particular, I would hope that we could learn something interesting about what kind of reasoning is allowed in such an empirically starved research program. In particular, what I’d like to know is:
What argumentative moves are licit in response to the cosmic acceleration problem?
As a first step toward figuring this out, I made a map of the most common arguments being made. To see my map, click the image on the left (or download the PDF). This map is inspired by a (much smaller) such diagram given by Sean Carroll (2003). Suggestions are more than welcome!
Soul Physics is authored by Bryan W. Roberts. Thanks for subscribing.
Want more Soul Physics? Try the Soul Physics Tweet.
Cool chart. So, here’s a question: What does it mean to say that “c is not constant”?
I’ve always been confused when people talk this way. It seems to me that ‘c’ is simply part of the spacetime geometry. Thoughts?
John,
Why can’t c change over the manifold of spacetime? Can’t one define a metric on the manifold such that c isn’t constant?
(I only started learning GR a few months ago, so sorry if this is a mathematically stupid question.)
Here’s one way to voice this kind of worry. A typical model of general relativity has three parts: a manifold, a metric, and a set of matter fields (all with certain suitable properties). We might assume that the Universe itself is represented by one of these models (insofar as these models are the appropriate way to describe the world). So the Universe itself has a concrete metric structure g_ab — and in principle, we could write it down once and for all, if only we were clever enough.
Now, in general, the metric determines the light cone structure in a model of GR. Conversely, if we observe a particular light cone structure, then we can recover the metric (after all, what we can actually *observe* is geodesic deviation, not the metric itself).
So what does it mean to say that light-cone structure can change? By the lights of the above description, it means that we have failed to fix g_ab. And that would mean that we don’t have a fixed model in the first place. An account of the Universe in which c varies is (by these lights) one in which we have failed to pick out a model of the Universe.
However, this doesn’t mean that the idea is utterly senseless. We easily broaden our notion of what a “model of GR” is. That’s what bi-metric approaches to quantum gravity try to do, for example. One defines two metrics for a given model, and then assumes that each one holds on a different scale. (One metric is for small scales, the other for very large scales.) You can still think of these two metrics as defining two distinct to two “speeds” of light. And they each define the “geometry of spacetime” in different regimes.
More general VSL theories occupy a small corner of debate on the arXiv. But: my own opinion is that, once you start messing with the fundamental constants, it’s a sign that you’ve really lost your way!
This was not exactly what I had in mind when I asked my question, but here’s one VSL theory in which c varies over spacetime (instead of across scales). They ensure that c does not appear explicitly in the metric by using a ‘spatial’ coordinate x^0 instead of t in the expression for the metric. Properties like covariance are unaffected so long as x^0 is used. They argue that the postulate that c is constant across spacetime is not a unit-independent postulate, and they define c in terms of measurement processes, so that a change of units in space and/or time can lead to non-constant c over spacetime.