Group Theory Of Your Spine
In more examples of the unreasonable effectiveness of mathematics, there now exists a robust application of group theory to the human spinal cord.
Modeling the Human Spine. A few years ago, Australian DOD scientist Dr. Vladimir Ivancevic unveiled a new model of the human spine. The model, called the Human Biodynamics Engine, was designed to study how various stresses (like those on a soldier carrying a load) can result in spinal injury. However, while older models were built up from the physics of compression, bending and shear, Ivancevic built his model using group theory. He published his result last week on the arXiv.
The ‘Spinal Cord’ Group. The central idea is to describe the degrees of freedom of each vertebrae using a group. The group that does the trick turns out to be the Special Euclidean Group SE(3). SE(3) is equivalent to the direct product group SO(3) ⊗ R3, which is just the group of rotations around a fixed point:
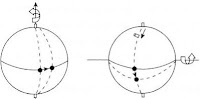
together with the group of spatial translations:

(both in three dimensions).
Makes sense, right? Those are the degrees of freedom of a piece of your spine. From there, it’s easy to model the spinal cord as one big direct product group, made up of as many copies of SE(3) as there are vertebrae.
Of course, to make this idea useful, Ivancevic must argue that most spinal injuries are due to what he calls an ‘SE(3)-jolt.’ This is, effectively, a certain kind of local perturbation of the forces acting on the ‘spinal cord’ group. However, if the data continues to support Ivancevic’s hypothesis, then he may have discovered a very useful new way to think about these injuries.
History: Applications of Groups. Mathematical groups began their history in the early 19th century, as a play-thing for pure mathematicians. Abel and Galois famously used them to study the roots of polynomials (especially the quintic).
Since then, applications of group theory have turned up in unexpected places. Group theory became inseparable from the study of both quantum theory and relativity in the mid-20th century, leading Wigner to famously call mathematics in general “unreasonably effective.” (I recommend Octavio Bueno’s very informative analysis of this history.)
In the last two decades, applications of group theory have surfaced in biology and in medicine as well. For example, groups have been applied to population genetics, epidemiology, neurobiology, and even anesthesiology. However, few of these applications have been very robust. Most deal only with combinatorial facts about the symmetric group Sn, the group of permutations of n objects.
Soul Physics is authored by Bryan W. Roberts. Thanks for subscribing.
Want more Soul Physics? Try the Soul Physics Tweet.
.jpg)